Much of neuroscience is based on scientific concepts but there are ways to mathematically depict this information. In this article, we will explore the equations that represent the interaction between ions that cause the action potential to ripple down a cell's axon.
Nernst Equation
The Nernst equation is used to determine the equilibrium potential of an ion. This tells you the electrical potential at which the electrical pull and the chemical pull balance each other out.
In order to understand this concept, we need to understand the electrochemical force that is changing the flow of ions.
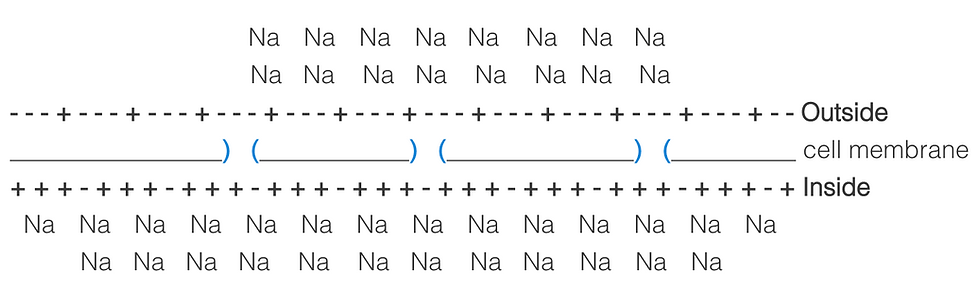
Let us take Na+ as an example. The inside of the cell is more electronegative than the outside of the cell. In addition, there are more Na+ ions outside the cell than inside the cell.
Since there are open ion channels in the cell membrane, this will allow the membrane to be selectively permeable to Na+.
Due to diffusion, the Na+ ions will flood the ion channels and enter the cell. This will change the charge on the inside and the outside of the cell. The inside of the cell will become more positive, although not as positive as the outside of the cell originally was. The outside of the cell will become more negative, but again not as negative as the inside of the cell originally was.
However, now that the inside of the cell is positively charged, it will repel the Na+ ions and they will flow down the ion channels back outside.
These two forces will pull and push the ions in opposite directions as the more ions flow into the cell, the more they will be repelled out.
Equilibrium can only be reached when the two forces are equal. The electrical potential of the cell at this point is what is calculated by the Nernst equation.
Below is the Nernst Equation:
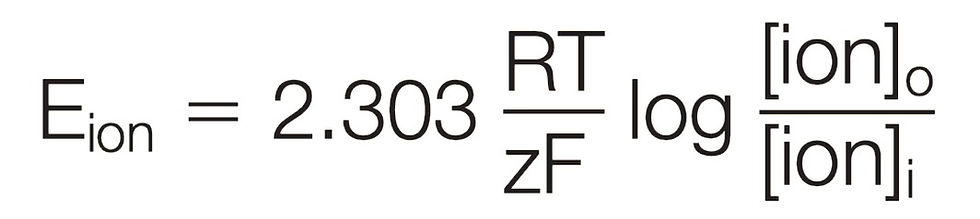
Let's break down all of the variables in this equation and simplify the situation.
E(ion): the ionic equilibrium potential.
R: Gas Constant [8.3145 J/(mol)(K)]
T: Temperature in Kelvin
z: charge of the ion {IMPORTANT: INCLUDE SIGNS}
F: Faraday's constant [ 96485 C/mol]
[ion](outside): the ionic concentration of the particular ion outside the cell
[ion](inside): the ionic concentration of the particular ion inside the cell
This may seem overwhelming but you are often given many of these values. To make it even simpler, many neuroscience classes use a standard temperature of 37 degrees Celsius for all problems. This allows us to simplify the equation to:
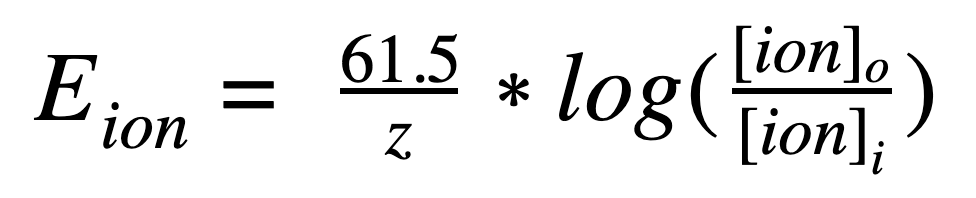
However, this equation alone is not enough to convey all of the information regarding membrane potential in a neuron. All of the ions in a cell work together and the Nernst equation only address the equilibrium potential of one ion. In next week's post, we will go explore the Goldman equation which can determine the resting potential of a cell while taking into account all ions.
Resources:
Bear, M. F., Connors, B. W., & Paradiso, M. (2016). Neuroscience: Exploring the brain. Wolters Kluwer.
Bình luận